
迹线微分方程 dx=u,dt dy=u dt dz=u,dt ·在欧拉观点下求迹线,因须跟定液体质点,此时欧拉变数 x,y,z成为1的函数,所以迹线的微分方程为 dx dy dz =dt 4[t)),zt),t1u,[x)0),zt),t1u[xt0)),z0,t] 这是由三个一阶常微分方程组成的方程组,未知变量为质点 位置坐标(x,八,z),它是1的函数。给定初始时刻质点的位 置坐标,就可以积分得到迹线

流线微分方程 ·流线是流速场的矢量线,是某瞬时对应的流场中的一条曲 线,该瞬时位于流线上的液体质点之速度矢量都和流线相切。 流线是与欧拉观点相对应的概念。有了流线,流场的空间分布 情况就得到了形象化的描绘

绕过机翼剖面的流线
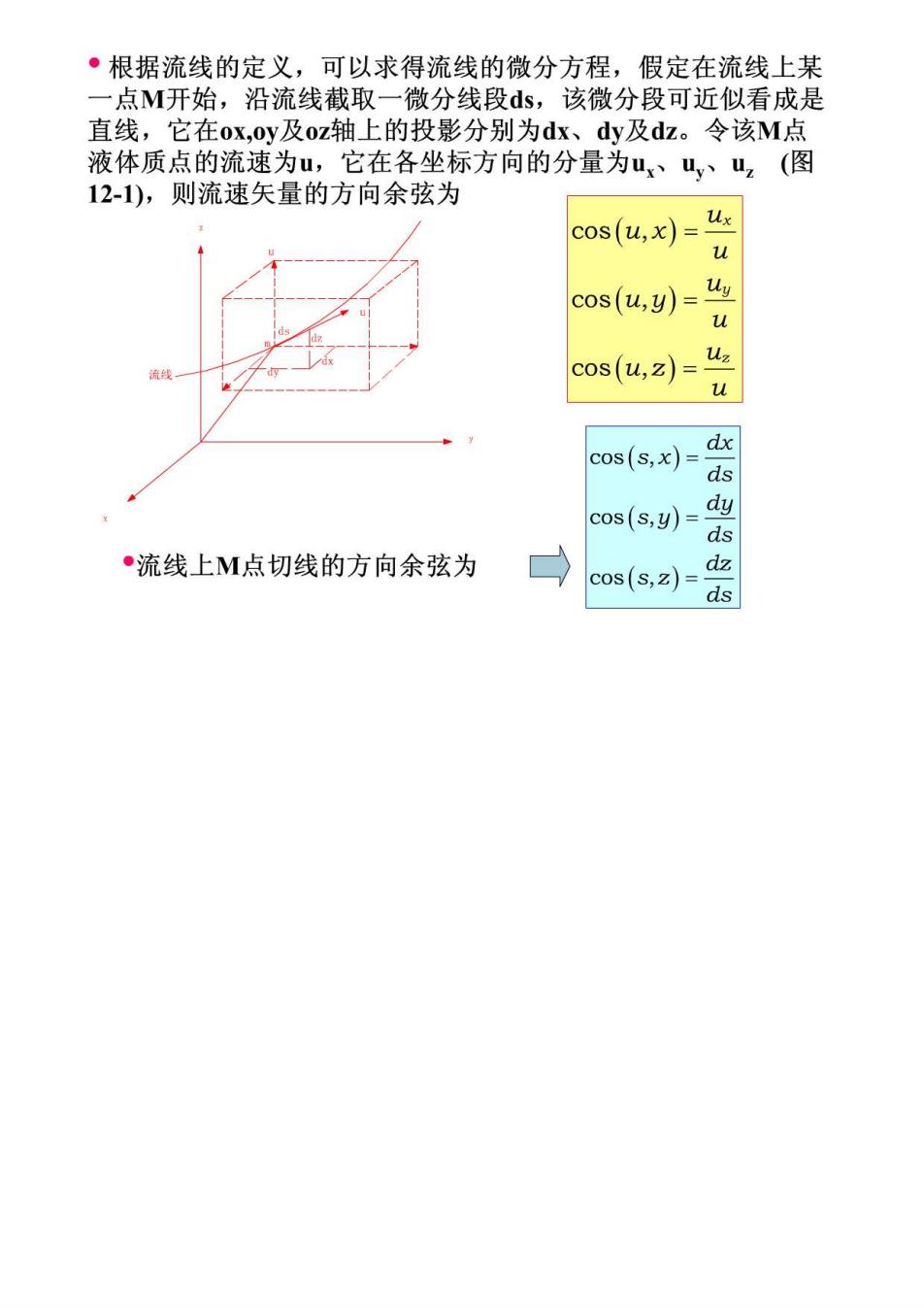
·根据流线的定义,可以求得流线的微分方程,假定在流线上某 一点M开始,沿流线截取一微分线段ds,该微分段可近似看成是 直线,它在ox,oy及oz轴上的投影分别为dx、dy及dz。令该M点 液体质点的流速为u,它在各坐标方向的分量为u,、山,、山z(图 12-1),则流速矢量的方向余弦为 cos(u,x)=u cos(u,y)=uu cos(u,2)=uz u cos(s,x)= dx ds cos(sy)=dy ·流线上M点切线的方向余弦为 cos(s,z)-dz

·因流线上每一点的流速向量与流线相切,故有 4-,业=四,业=地 u ds' u ds' u ds 口 dx dy dz ds u,(x,y,z,t)u(x,y,z,t)u(x,y,z,t)u 实际上这是两个微分方程,其中1是参数。可求解得到两族 曲面,它们的交线就是流线族