
3.1热力学性质间的关系 3.1.1热力学基本方程 3.1.2点函数间的数学关系式 3.1.3 Maxwell关系式 3.1.4其它重要的热力学关系式 —Maxwell:关系式的应用 7
3.1 热力学性质间的关系 3.1.1 热力学基本方程 3.1.2 点函数间的数学关系式 3.1.3 Maxwell关系式 3.1.4 其它重要的热力学关系式 ——Maxwell关系式的应用 7

3.1.1热力学基本方程 根据热力学第一、第二 dU Tds-pdv (3-1) 定律,对单位质量定组 成的均匀流体,在非流 dH =TdS+Vdp 3-2) 动状态下,不考虑动、 dA=-pdy-SdT 3-3) 位能的变化,可推出其 热力学性质间的关系。 dG=Vdp-SdT (3-4) 即“物化”讲过的四大 热力学基本方程 微分方程 适用于定组成的均相流体。 惟真帷實
根据热力学第一、第二 定律,对单位质量定组 成的均匀流体,在非流 动状态下,不考虑动、 位能的变化,可推出其 热力学性质间的关系。 即“物化”讲过的四大 微分方程 3.1.1 热力学基本方程 dU TdS pdV dH TdS Vdp dA pdV SdT dG Vdp SdT (3-2) (3-3) (3-4) (3-1) 热力学基本方程 适用于定组成的均相流体

注意几点: ◆封闭或定组成的敞开体系均适用; ◆均相体系(单相); ◆平衡态间的变化 常用于1摩尔时的性质。式中容量性质为单位质量或单位 摩尔的量,即强度性质 9 惟真帷實
注意几点: 封闭或定组成的敞开体系均适用; 均相体系(单相); 平衡态间的变化; 常用于1摩尔时的性质。式中容量性质为单位质量或单位 摩尔的量,即强度性质 9

如何计算U、H、A、G? 1)UH、A、G=fp,V,T,S) dU Tds-pdy 2)p,V,T,S中只有两个是独立变量。S不能直接 dH TdS+Vdp 测定,以(T,p)和(T,)为自变量最有实际意义。 dA=-pdV-SdT 3) 若有S=S(T,p)和V=V(T,p),就能推算不可直 dG=Vdp-SdT 接测量的U、H、A、G。 问题:如何建立V=V(T,p)和S=S(T,p)? >建立V=(T,p),用EOS。 >通过Maxwell关系式建立S=S(T,p),使难测量 与易测量联系起来。 惟真帷竇
如何计算U、H、A、G? 1) U、H、A、G = f (p,V,T,S) 2) p,V,T,S中只有两个是独立变量。S不能直接 测定,以(T,p)和(T,V)为自变量最有实际意义。 3) 若有S =S(T,p)和V=V(T,p),就能推算不可直 接测量的U、H、A、G。 问题:如何建立V=V(T,p)和S =S(T,p)? 建立V=V(T,p),用EOS。 通过Maxwell关系式建立S =S(T,p),使难测量 与易测量联系起来。 G V p S T A p V S T H T S V p U T S p V d d d d d d d d d d d d
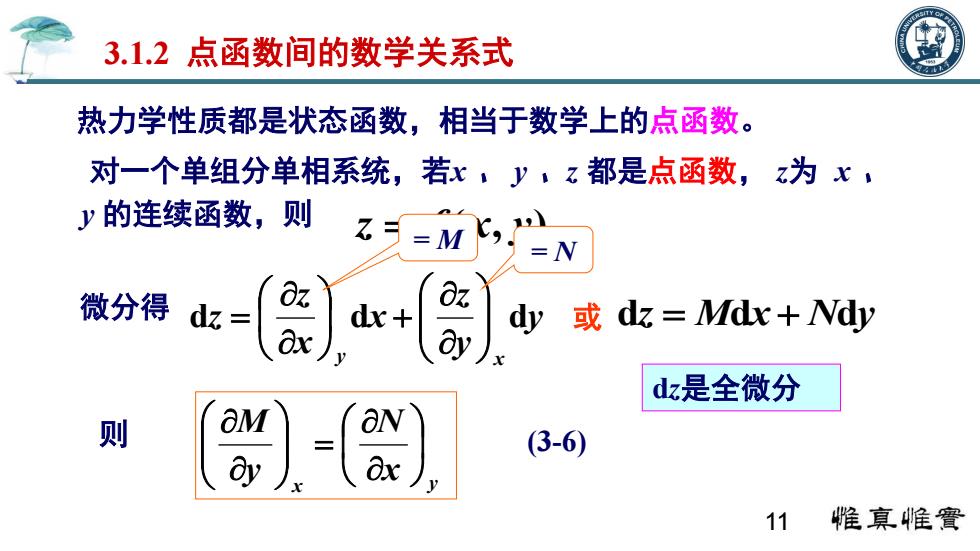
3.1.2点函数间的数学关系式 热力学性质都是状态函数,相当于数学上的点函数。 对一个单组分单相系统,若x,y,z都是点函数,z为x, y的连续函数,则 9=M -N 微分得 dz= dx+ Oz dy 或dk=Mdx+Nd ax ay) dz是全微分 则 OM aN (3-6) 11 膣真帷實
热力学性质都是状态函数,相当于数学上的点函数。 对一个单组分单相系统,若x 、 y 、z 都是点函数, z为 x 、 y 的连续函数,则 z f (x, y) 3.1.2 点函数间的数学关系式 微分得 y y z x x z z y x d d d dz Mdx Ndy x y x N y M 则 dz是全微分 = M = N (3-6) 或 11