
其压力p为 p-月 (1-5) 根据分子运动论,气体的压力是气体分子运动撞击表面,而在单位面积上所呈现的垂直 于壁面的平均作用力, p-受 式中,为单位容积内的分子数,2为分子的平均移动动能。液体系统除传递压力 外,在重力场中还有由于液体的重最 而产生的静压力。静压力与液柱的垂直高度有关。 1.压力的测量、表压力和绝对压力 流体的压力用压力计测量。工程上常用的压力计有两种,即弹簧管压力计及测量微小压 力的U形管压力计。它们实际上是测量压差的仪器,故又称压差计。 弹簧管压力计的基本结构如图1一1所示。它利用弹簧管在内外压差作用下产生变形, 从而拨动指针转动来指示工质与环境间的压差
其压力 p 为 A F p = (1-5) 根据分子运动论,气体的压力是气体分子运动撞击表面,而在单位面积上所呈现的垂直 于壁面的平均作用力, 3 2 2 2 0 mw p = n 式中, n0 为单位容积内的分子数, 2 2 mw 为分子的平均移动动能。液体系统除传递压力 外,在重力场中还有由于液体的重量 而产生的静压力。静压力与液柱的垂直高度有关。 1.压力的测量、表压力和绝对压力 流体的压力用压力计测量。工程上常用的压力计有两种,即弹簧管压力计及测量微小压 力的 U 形管压力计。它们实际上是测量压差的仪器,故又称压差计。 弹簧管压力计的基本结构如图 1-1 所示。它利用弹簧管在内外压差作用下产生变形, 从而拨动指针转动来指示工质与环境间的压差

图1一】弹簧管压力计 图1一2U形管压力计 U形管压力计如图1一2所示,其主要部件为一U形玻璃管,管内盛有用来测压的 液体,例如水银或水。·形管的一端与被测系统相连,另一端与环境(例如大气)相通。当系 统压力与环境压力不等时,即可由U形管两边液柱的高度差读出系统与环境之间的压差。 根据流体静力学原理,在连通容器内同一高度上的压力相等。于是,对于A一A等压面 可写出力平衡方程如下: p=Ps +pgH 或 (1-6) 式中:H为U形管两边的液柱高度差,■: p为被测系统的压力,Pa: P为环境压力(一般情况下为大气压),Pa
图 1—1 弹簧管压力计 图 1—2 U 形管压力计 U 形管压力计如图 1-2 所示,其主要部件为一 U 形玻璃管,管内盛有用来测压的 液体,例如水银或水。U 形管的一端与被测系统相连,另一端与环境(例如大气)相通。当系 统压力与环境压力不等时,即可由 U 形管两边液柱的高度差读出系统与环境之间的压差。 根据流体静力学原理,在连通容器内同一高度上的压力相等。于是,对于 A -A 等压面 可写出力平衡方程如下: p = pb + ρgH 或 g p p H b ρ − = (1-6) 式中: H 为 U 形管两边的液柱高度差,m; p 为被测系统的压力,Pa; pb 为环境压力(一般情况下为大气压力),Pa;

P为测压液体的密度,kg/ 8为重力加速度,m/s 由式(1-6)可见,当选定测压液体,且将P,8视为常数时,液柱高度差H与压差 (P一P)成正比,故可用高度差H单值地度量压差Ap。这就是U形管压差计的工作原 理。式(1-6)反映了压力与液柱高度差H间的数量关系。 工程上常用水或水银作为测压液体,其密度随温度变化而变化。它们在4℃及0℃时的 密度分别为 Puoucy =10'kg/m Ps00=13.595g1m 同时假定重力加速度8为常数,其数值为 g=9.80665m/s2 在公制中,P8称为重度,用Y表示。水在4℃,水银在0℃时的重度分别为 Ym,o4rg=1000kg1m3=9806N/m Y6re=l3595kgr1m3=13321w1m 当水的温度不为4℃或水银的温度不为0℃时,液体密度P发生变化,但在工程近似计算 中常忽略P随温度的变化而仍取上述数值
ρ 为测压液体的密度,kg/m3 ; g 为重力加速度, 2 m / s . 由式(1-6)可见,当选定测压液体,且将 ρ, g 视为常数时,液柱高度差 H 与压差 ( b p − p )成正比,故可用高度差 H 单值地度量压差 Δp 。这就是 U 形管压差计的工作原 理。式(1-6)反映了压力与液柱高度差 H 间的数量关系。 工程上常用水或水银作为测压液体,其密度随温度变化而变化。它们在 4℃及 0℃时的 密度分别为 3 3 (4 ) 10 / 2 kg m H O C ρ o = 3 (0 ) 13.595kg / m Hg C ρ o = 同时假定重力加速度 g 为常数,其数值为 2 g = 9.80665m /s 在公制中, ρg 称为重度,用 γ 表示。水在 4℃,水银在 0℃时的重度分别为 3 3 (4 ) 1000 / 9806 / 2 kgf m N m H O C γ o = = 3 3 (0 ) 13595kgf / m 133321N / m Hg C γ o = = 当水的温度不为 4℃或水银的温度不为 0℃时,液体密度 ρ 发生变化,但在工程近似计算 中常忽略 ρ 随温度的变化而仍取上述数值
由以上分析可见,由于测压仪表本身常处于大气压力的作用下,表上所指示的压力并非 被测系统的真实压力,而是系统压力与当时当地大气压力的差值:称为表压九,用P·表示。 系统的真实压力称为绝对压力,用P表示。表压力与绝对压力之间有以下关系。 1)p>P时 p=P.+ps (1-7) 式中,P为当时当地大气压力,P及P:分别为系统的绝对压力及表压力。 (②)P<P时 此时测量压力的仪表叫真空计。真空计上的读数称为真空度,用P表示,如图1一3所示。 此时有 P=P-P, (1-8) 图1-3真空计 图1-4绝对压力与表压力 若以绝对压力为0时作为基线,则可将表压力、真空度、绝对压力、大气压力之间的关 系用图1-4表示。 由以上论述可见,为确定系统的压力除使用压力计外还应同时使用大气压力计以确定当
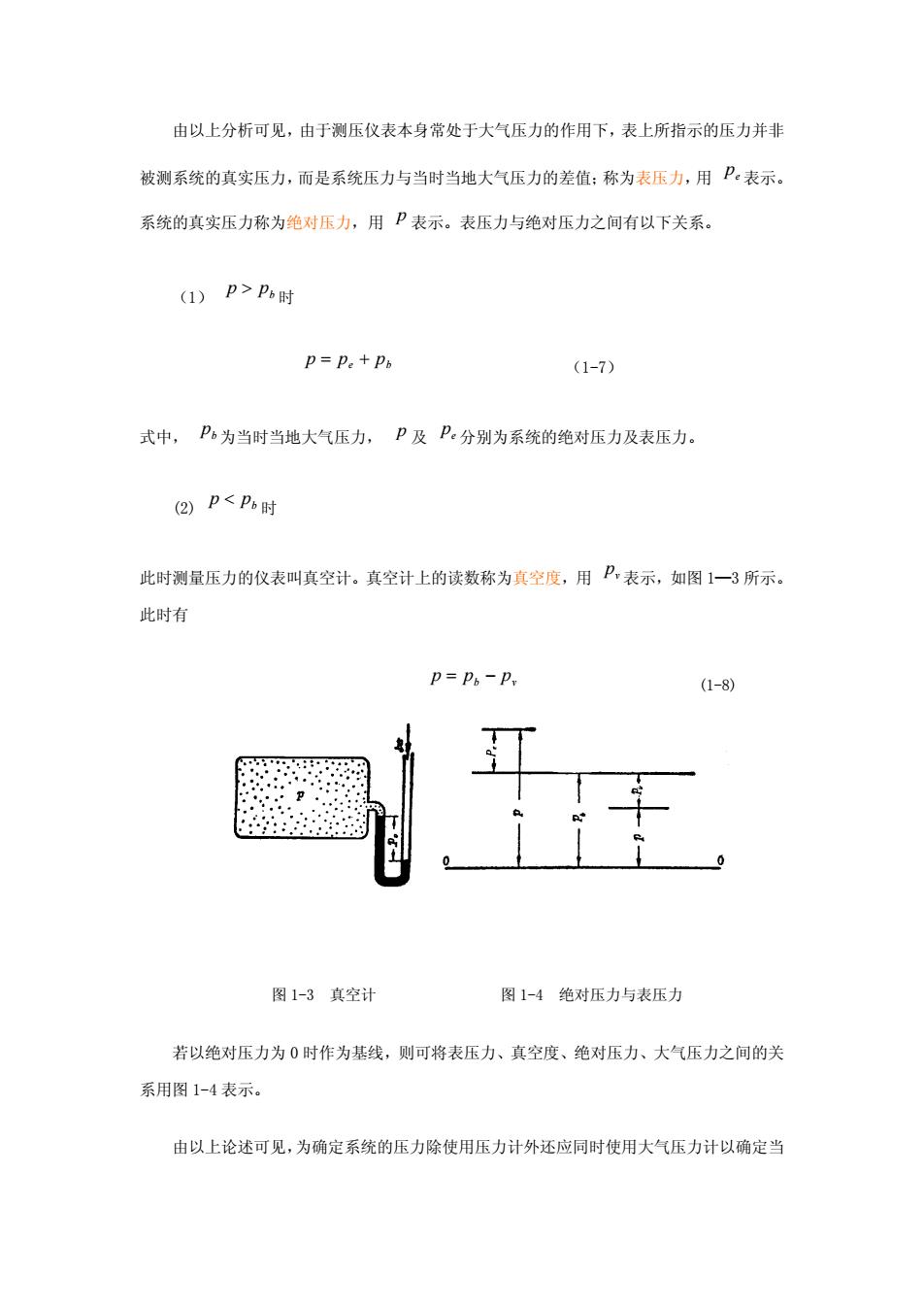
由以上分析可见,由于测压仪表本身常处于大气压力的作用下,表上所指示的压力并非 被测系统的真实压力,而是系统压力与当时当地大气压力的差值;称为表压力,用 e p 表示。 系统的真实压力称为绝对压力,用 p 表示。表压力与绝对压力之间有以下关系。 (1) b p > p 时 p = pe + pb (1-7) 式中, b p 为当时当地大气压力, p 及 e p 分别为系统的绝对压力及表压力。 (2) b p < p 时 此时测量压力的仪表叫真空计。真空计上的读数称为真空度,用 v p 表示,如图 1—3 所示。 此时有 b v p = p − p (1-8) 图 1-3 真空计 图 1-4 绝对压力与表压力 若以绝对压力为 0 时作为基线,则可将表压力、真空度、绝对压力、大气压力之间的关 系用图 1-4 表示。 由以上论述可见,为确定系统的压力除使用压力计外还应同时使用大气压力计以确定当

时当地的大气压力。由于大气压力变化不大,当绝对压力较大时,大气压力数值的变化相对 地说影响甚小,这时在工程计算上可将大气压力视为常数。但当被测系统压力较小,其数值 与大气压力相近时,则不能将大气压力视为常数而应利用大气压力计测定其具体数值。 作为工质的状态参数,应该是P而不是P或P,。 2.压力的单位 在法定计量单位中压力的单位由基本单位导出。根据牛顿第二定律 F=阳 法定计量单位中规定,四为1kg、a为1回/s、F为1N时,由此导出的压力单位,称为帕斯 卡,单位符号为Pa。在工程应用上常嫌Pa过小,而用Pa(即10Pa)作为压力单位。习惯上 曾用巴(符号为bar,1bar=10Pa)作为压力单位。 在公制单位中,压力用工程气压(at)作单位: lat=lkgf/cm'=10'kgf/m 在工程计算中,当系统的绝对压力远大于大气压力时,常在式(1-)中将大气压力视为 定值,并取值为0.1Pa或1at。 物理学中,把纬度45°的海平面上的常年平均气压定作标准大气压。标准大气压在气压 计上的水银柱高度为760mm,它相当于0.1013MPa或1.03323at。 物理学上规定,压力为1标准大气压、温度为0℃的状况称为物理标准状况。各种压力 单位的换算关系主要有 1MPa=10bar=10.1972工程气压 1.2.3温度及热力学第零定律 温度是衡量物体冷热程度的物理量,在热力学分析中至关重要
时当地的大气压力。由于大气压力变化不大,当绝对压力较大时,大气压力数值的变化相对 地说影响甚小,这时在工程计算上可将大气压力视为常数。但当被测系统压力较小,其数值 与大气压力相近时,则不能将大气压力视为常数而应利用大气压力计测定其具体数值。 作为工质的状态参数,应该是 p 而不是 e p 或 v p 。 2.压力的单位 在法定计量单位中压力的单位由基本单位导出。根据牛顿第二定律 F =ma 法定计量单位中规定,m 为 1kg、a 为 1m/s2 、F 为 1N 时,由此导出的压力单位,称为帕斯 卡,单位符号为 Pa。在工程应用上常嫌 Pa 过小,而用 MPa(即 106 Pa)作为压力单位。习惯上 曾用巴(符号为 bar,1bar=105 Pa)作为压力单位。 在公制单位中,压力用工程气压(at)作单位: 1at=1kgf/cm2 =104 kgf/m2 在工程计算中,当系统的绝对压力远大于大气压力时,常在式(1-7)中将大气压力视为 定值,并取值为 0.1MPa 或 1at。 物理学中,把纬度 45o 的海平面上的常年平均气压定作标准大气压。标准大气压在气压 计上的水银柱高度为 760mm,它相当于 0.1013MPa 或 1.03323at。 物理学上规定,压力为 1 标准大气压、温度为 0℃的状况称为物理标准状况。各种压力 单位的换算关系主要有 1MPa=10bar=l0.1972 工程气压 1.2.3 温度及热力学第零定律 温度是衡量物体冷热程度的物理量,在热力学分析中至关重要