
Nuclear Magnetic Resonance-Bushberg Chapter 14 Diagnostic Radiology Imaging Physics Course Resonance and Excitation Changing Reference Frames M-Longhudinal Magetization 67 E .Why is MRI so hard to learn? .Changing reference frames M Classical versus Quantum 胎 Mechanical explanation .Lab and rotating frames 成 ◆Changing scales 品 。Macroscopic Intermediate(spin isochromats) mm 马家 ha vo 180 then split up later into smaller and smaller pieces 4a Resonance and Excitation Resonance and Excitation .B,field component rotating at Larmor f (off-freg.-litle effect) Time required 10-100 usec .Rotating reference frame:B,stationary in x-y plane B,applied torque to Mrotation:B ◆90°pulse一largest My (signal)generated describes the on th ◆For flip angle(g<90 。smaller M gneri Common angles:90(/2 radians:/2 pulse)and 180(radians) ◆less time necessary to displace M 9,19and26May2005 6
Nuclear Magnetic Resonance – Bushberg Chapter 14 Diagnostic Radiology Imaging Physics Course 9, 19 and 26 May 2005 6 © UW and Brent K. Stewart, PhD, DABMP 21 Resonance and Excitation c.f. Bushberg, et al. The Essential Physics of Medical Imaging, 2nd ed., p. 382. RF Pulse Angle Tip: 0° 90° 180° Higher energy state © UW and Brent K. Stewart, PhD, DABMP 22 Changing Reference Frames Changing Reference Frames Why is MRI so hard to learn? Changing reference frames Classical versus Quantum Classical versus Quantum Mechanical explanation Lab and rotating frames Changing scales Macroscopic Intermediate (spin Intermediate (spin isochromats) Microscopic/QM Start with a voxel of 1 mm x 1 mm Start with a voxel of 1 mm x 1 mm x 10 mm as a starting point and x 10 mm as a starting point and then split up later into smaller and then split up later into smaller and smaller pieces © UW and Brent K. Stewart, PhD, DABMP 23 Resonance and Excitation B1 field component rotating at Larmor f field component rotating at Larmor f0 (off-freq. → little effect) little effect) Rotating reference frame: B1 stationary in x-y plane B1 applied torque to applied torque to Mz → rotation: rotation: θ = γ · B1· t Flip angle ( Flip angle (θ) describes the rotation through which the longitudinal ) describes the rotation through which the longitudinal magnetization (Mz) is displaced to generate transverse ) is displaced to generate transverse magnetization (Mxy) Common angles: 90° (π/2 radians: /2 radians: π/2 pulse) and 180° (π radians) radians) c.f. Bushberg, et al. The Essential Physics of Medical Imaging, 2nd ed., p. 384. Rotating Frame Lab Frame © UW and Brent K. Stewart, PhD, DABMP 24 Resonance and Excitation Time required 10-100 µsec 90° pulse → largest Mxy (signal) generated For flip For flip angle ( angle (θ) < 90° smaller Mxy component component generated and less signal generated and less signal less time necessary to less time necessary to displace Mz greater amount of greater amount of Mxy (signal) (signal) per excitation time Low flip Low flip angle (θ) very important in rapid MRI important in rapid MRI scanning c.f. Bushberg, et al. The Essential Physics of Medical Imaging, 2nd ed., p. 384
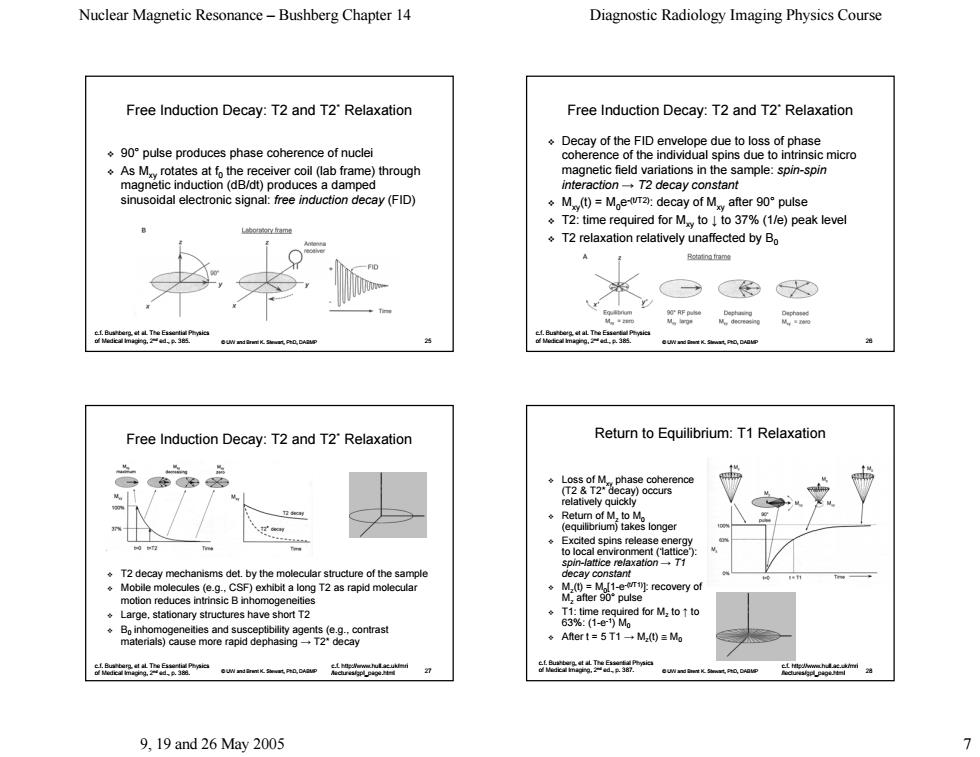
Nuclear Magnetic Resonance-Bushberg Chapter 14 Diagnostic Radiology Imaging Physics Course Free Induction Decay:T2 and T2'Relaxation Free Induction Decay:T2 and T2'Relaxation Decay of the FID envelope due to loss of phase ◆9o°oulse produces phase coherence of nuclei coherence of the individual spins due to As Mrotates at fo the receiver coil (lab frame)through magnetic field variations in the sample:spin-spin magnetic induction(dB/dt)produces a damped interaction-T2 decay constant sinusoidal electronic signal:free induction decay(FID) ÷M)-M,ewr2a:decay of M after90°pulse T2:time required for Mto to 37%(1/e)peak level o9m T2 relaxation relatively unaffected by Bo Bontno fram 咖 色W Free Induction Decay:T2 and T2'Relaxation Return to Equilibrium:T1 Relaxation cay)occurs elatively quickly spin-lattice relaxationT1 .T2 decay mechanisms det.by the molecular structure of the sample .Mobile molecules (e.g.CSF)exhibit a long T2 as rapid molecular motion reduces intrinsic B inhomogeneities Large stationary structures have short t2 ◆Aftert=5T1一M)=Mo 品ma 9.19and26May2005 >
Nuclear Magnetic Resonance – Bushberg Chapter 14 Diagnostic Radiology Imaging Physics Course 9, 19 and 26 May 2005 7 © UW and Brent K. Stewart, PhD, DABMP 25 Free Induction Decay: T2 and T2* Relaxation 90° pulse produces phase coherence of nuclei pulse produces phase coherence of nuclei As Mxy rotates at f rotates at f0 the receiver coil (lab frame) through the receiver coil (lab frame) through magnetic induction (dB/dt) produces a damped magnetic induction (dB/dt) produces a damped sinusoidal electronic signal: sinusoidal electronic signal: free induction decay (FID) c.f. Bushberg, et al. The Essential Physics of Medical Imaging, 2nd ed., p. 385. © UW and Brent K. Stewart, PhD, DABMP 26 Free Induction Decay: T2 and T2* Relaxation Decay of the FID envelope due to loss of phase Decay of the FID envelope due to loss of phase coherence of the individual spins due to intrinsic micro coherence of the individual spins due to intrinsic micro magnetic field variations in the sample: magnetic field variations in the sample: spin-spin interaction interaction → T2 decay constant T2 decay constant Mxy(t) = M0e-(t/T2): decay of Mxy after 90° pulse T2: time required for Mxy to ↓ to 37% (1/e) peak level to 37% (1/e) peak level T2 relaxation relatively unaffected by B0 c.f. Bushberg, et al. The Essential Physics of Medical Imaging, 2nd ed., p. 385. © UW and Brent K. Stewart, PhD, DABMP 27 Free Induction Decay: T2 and T2* Relaxation T2 decay mechanisms det. by the molecular structure of the sampl T2 decay mechanisms det. by the molecular structure of the sample Mobile molecules (e.g., CSF) exhibit a long T2 as rapid molecular motion reduces intrinsic B inhomogeneities Large, stationary structures have short T2 B0 inhomogeneities and susceptibility agents (e.g., contrast inhomogeneities and susceptibility agents (e.g., contrast materials) cause more rapid dephasing materials) cause more rapid dephasing → T2* decay c.f. Bushberg, et al. The Essential Physics of Medical Imaging, 2nd ed., p. 386. c.f. http://www.hull.ac.uk/mri /lectures/gpl_page.html © UW and Brent K. Stewart, PhD, DABMP 28 Return to Equilibr Return to Equilibrium: T1 Relaxation Loss of Mxy phase coherence phase coherence (T2 & T2* decay) occurs (T2 & T2* decay) occurs relatively quickly Return of Mz to M0 (equilibrium) takes longer (equilibrium) takes longer Excited spins release energy Excited spins release energy to local environment (‘lattice’): to local environment (‘lattice’): spin-lattice relaxation lattice relaxation → T1 decay constant decay constant Mz(t) = M0[1-e-(t/T1)]: recovery of : recovery of Mz after 90° pulse T1: time required for Mz to ↑ to 63%: (1-e-1) M0 After t = 5 T1 After t = 5 T1 → Mz(t) ≅ M0 c.f. Bushberg, et al. The Essential Physics of Medical Imaging, 2nd ed., p. 387. c.f. http://www.hull.ac.uk/mri /lectures/gpl_page.html